ゴリラと学ぶ「余弦定理」

ゴリたちゴリラ🦍も、ニンゲン👫も、器用なうでをもっているウホ。このきようなうでがあれば、なんでもできちゃうウホ。

でも、うでをつかってできないことも多いウホ。ふと思ったこととして、両うでをつかって、空中で手と手の間のきょりを知るにはどうすればいいウホ？

ふつうなら、定規📏をもったりして測ることが出来るウホ。つくえのうえに置いた定規にのせれば、うでとうでの間の距離は測ることができるウホ。
でも、くうちゅうで、なにももたないとき、どうやって測るウホ？

なんだかもやもやしてきたウホ！こんなときは問題として考えてみるにかぎるウホ。

---

もんだい

あるゴリラが、広げた腕と腕の間の距離をはかろうとしたウホ。よりただしくは、手と手の間の距離をはかろうとしたウホ。
これは空中ではかろうとしているから、つくえのうえに定規をおいてはかったりとかは出来ないとするウホ。

いま、ゴリラの腕の長さが1 mだとするウホ。これを、60°の角度にひらいているとするウホ。

このときの、ゴリラの手と手の間の距離は、どれくらいウホ？
ただし、ゴリラの胸の厚さはかんがえずに、1点から1 mの長さの直線が60°の開きで2本はえているとかんがえてほしいウホ。

🦍📐🦍📐🦍📐🦍📐🦍📐🦍📐

---

こたえ

別解もいろいろあるとおもうけど、ひとまずのかいとうを用意するウホ。 ニンゲンが高校数学でならう「余弦定理」をつかうウホ！ 正弦定理のほうは、まえに崖の上のゴリラでやったウホ。

余弦定理は、下みたいな定理だったウホ。

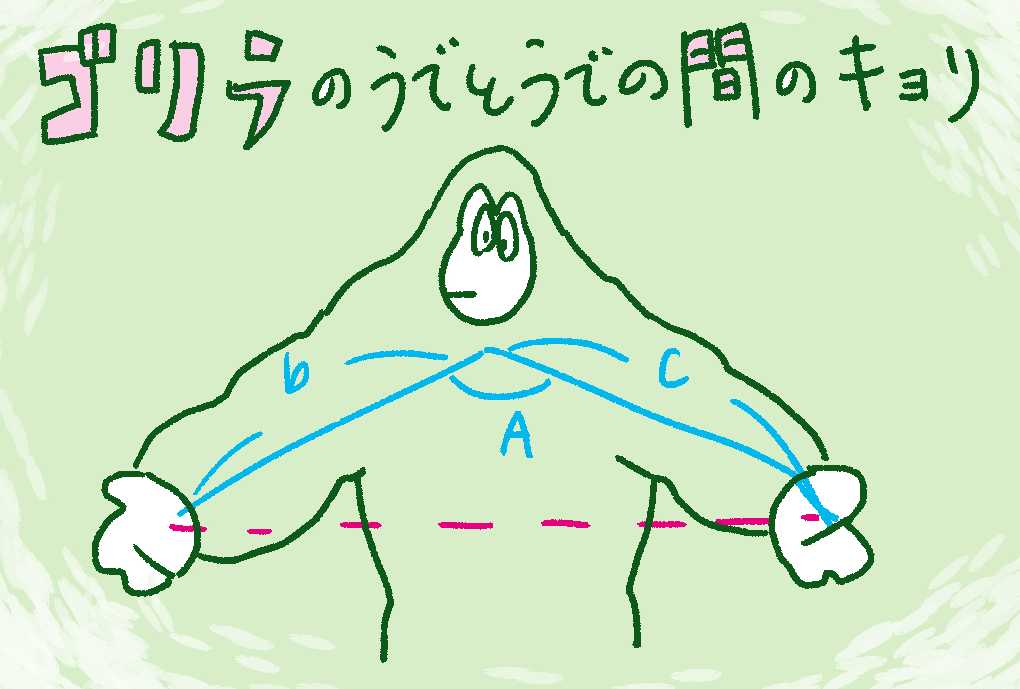
三角形ABCについて、
$A = 角A、B = 角B、C = 角C、$
$a = BCの長さ、b = CAの長さ、c = ABの長さ$
とすると、

$a^2 = b^2 + c^2 - 2bc\rm{cos}A$
$b^2 = c^2 + a^2 - 2bc\rm{cos}B$
$c^2 = a^2 + b^2 - 2bc\rm{cos}C$

しょうめいはめんどくさいから今回は省略するけど、これをつかうと求まるウホ！

うえのしきのどれでもいいけど、$a^2 = b^2 + c^2 - 2bc\rm{cos}A$をつかうことにするウホ。

いま、$b = c = 1 m$で、$b^2 + c^2 = 2$ウホ。
さらに、$\rm{cos}60° = \frac{1}{2}$だから、$- 2bc\rm{cos}A = -1になるウホ。$

したがって、$a^2 = b^2 + c^2 - 2bc\rm{cos}A = 1$

だから、$a = 1 m$になるウホ！

できた三角形は、正三角形になるウホ！

---

こたえ： 1 m

---

腕の長さと開く角度を知ることで、手と手の間の距離👐を知ることができたウホ。
でも、今度はあしとあしのあいだ👣の距離がきになってきちゃったウホ！
もっというと、片腕と腰とのあいだのきょり、首と肩のあいだのきょりまできになってきちゃったウホ！
もうやりつづけているときりがないから、これらについてはまたこんどやることにするウホ。