ゴリラと学ぶ学ぶ「正弦定理」二点の距離編

2人のゴリラがにらみあい🦍💥🦍をしているウホ。いまにもとびかからんばかりの敵意むきだし👿で、ののしり💥あっているウホ。
そんな様子を、ゴリもそのゴリラたちの近くでみている👀ウホ。 でも、ゴリを含めた3人のゴリラたちのまえには、けっこうおおきい崖（がけ）⛰があるウホ。 2人のゴリラは、この崖をとびこえないかぎり、戦うことはないウホ。

このゴリラたちは、崖をとびこえてたたかうことになるのか、考えてみるウホ。

もんだい

ゴリを含めて、3人のゴリラ（ゴリ、ゴリラA、ゴリラB）が三角形▲をつくるように立っているウホ。
ゴリラの前にはがけ⛰があって、けっこう深い🌌ウホ。ちゃんとむこうにとんでいける自信がなければ、とてもとびこえようとはおもわないウホ。

ゴリは、とてもラッキーなことに、ゴリのいるところからゴリラAまでのきょりを、偶然にもはかったことがあったウホ。
そのきょりは、6 mだったウホ。

そして、ゴリのもっていた分度器をつかって、ゴリラA-ゴリ-ゴリラBの角度（角ゴ）をはかったウホ。そのあと、ゴリラBに分度器をなげわたして、ゴリラA-ゴリラB-ゴリの角度（角B）をはかってもらったウホ。
そうすると、角ゴ = 61°、角B = 38°になったウホ。

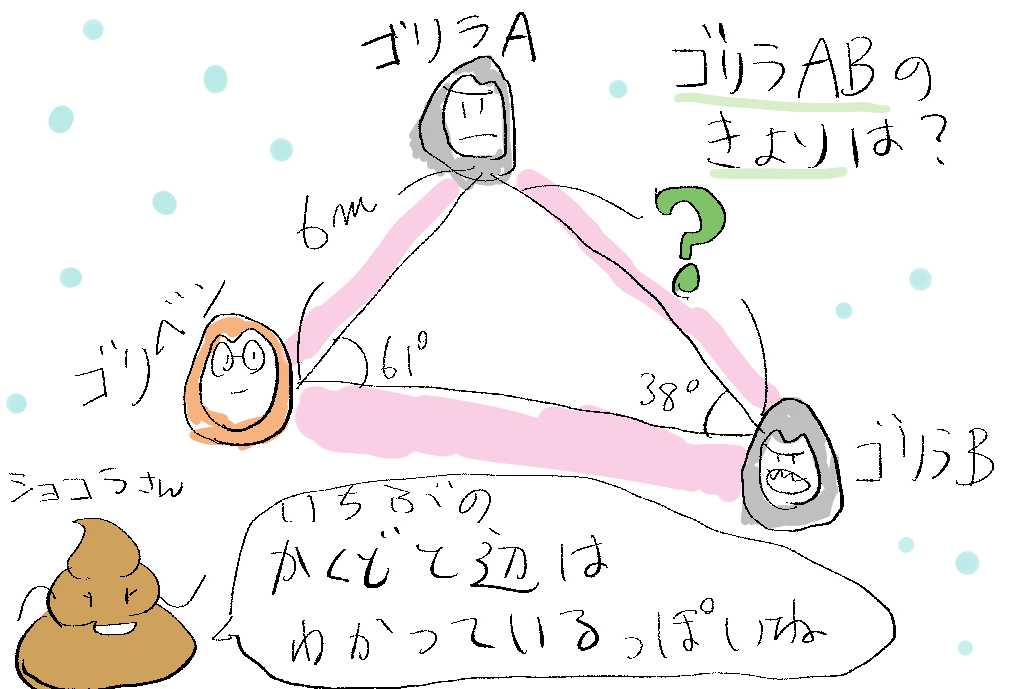
まずはこのときの、ゴリラAとゴリラBのきょりをかんがえてみてほしいウホ。
そして、ゴリラAが走りはばとびで9 mとべるとき、2人のゴリラはたたかうことができるか判断してほしいウホ。

ひつようなら、つぎの値を使っていいウホ。

$sin38° = 0.6157$
$sin61° = 0.8746$

🦍——🦍——🦍

---

こたえ

角度ときょりがわかっていて、直角三角形じゃないばあいのもんだいになるウホ。
こんなときは、正弦定理をつかってみるウホ。
正弦定理は、ニンゲンが高校数学でならう、次のような定理だったウホ。

$∠Aに対する辺の長さをa、$
$∠Bに対する辺の長さをb、$
$∠Cに対する辺の長さをcとするとき、$
$△ABCについて、外接円（外がわで接する円）の半径をRとすると、$
$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R$

今回は外接円の半径はおいといて、$\frac{a}{sinA} = \frac{b}{sinB}$のようなかんけいだけつかうウホ。 各辺をつぎのようなものにしておくウホ。

$b = ゴリからゴリラAまでのきょり$
$ゴ = ゴリラAからゴリラBまでのきょり$

わかっていることをかくと、
$b = ゴリからゴリラAまでのきょり = 6$
$sinゴ = sin38° = 0.6157$
$sinB = sin61° = 0.8746$

うえのしきを変形🤖してだいにゅうすると、
$ゴ = \frac{sinゴ}{sinB} × b = \frac{sin61°}{sin38°} × 6 = \frac{0.8746}{0.6157} × 6$

から、ゴリラAとゴリラBの距離は、約8.5 m（有効数字はてきとう）になるウホ。
ゴリラAの走りはばとびは9 mはとべるから、ゴリラAはぎりぎりゴリラBに届きそうだウホ！

---

こたえ：　ゴリラAとゴリラBのきょりは「約8.5 m」で、ゴリラAはぎりぎりゴリラBに届くウホ。

---

それなりの答えがだせて、ゴリ🦍はまんぞく😊したウホ。「ゴリラAはゴリラBとたたかえるウホ」と結果をつたえて、きぶんよくおうち🏠に帰るウホ。

何かおおきいものが二つ、崖の下におちた音がして、それっきり静かになったけど、気にしないで帰ったウホ。