ゴリラと学ぶ「二次関数」頂点編

ゴリはいつも、じぶんの似顔絵😀を書くときには、じぶんのあたまをなんとなく山なりにかいているウホ。でも、ほんとうにきちんと山なりな絵を書きたいときには、きっちりと数式であらわせられたらべんりウホ。まいかいおなじあたまをかくのもめんどうだし、もしかすると自動でゴリラを書けるようにもなるかもしれないウホ!
ニンゲンは、やまなりな図形をかきたいとおもったときには、いろいろかきかたはあるだろうけど、「二次関数」というものをつかうとおもうウホ。
まえにも、木の向こうのニンゲンに放物線上に茶色いねじねじ💩をなげるほうほうについてかんがえたときも、二次関数がかかわる投げ方をしていたウホ。この考え方をおうようすれば、ゴリのなめらかなやまなりあたまも数式であらわせるかもしれないウホ!
そんなこんなで、こんかいは二次関数の基礎にかんしてかんがえるウホ。
もんだい
ある二次関数で、頂点が(5, 25)となるようなグラフをかんがえるウホ。
このグラフは、ゴリのあたまみたいに、なだらかな山のような形をしていてほしいウホ。
そして、放物線は、原点(0, 0)に交点をもっていてほしいウホ。
この二次関数は、どういう式になるウホ?
y = なんとかxみたいなかたちであらわしてほしいウホ。
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
ニンゲンが高校数学でならう二次関数をやるウホ!
ちゅうがっこうでもならったかもしれないけど、そのちょっと発展したやつウホ。
中学校でならった二次関数は、放物線の頂点(山なりなグラフのいちばん高い(または低い)ところ)が原点、つまり(x, y) = (0, 0)だったウホ。
高校では、そこからはってんして、放物線のちょうてんをぐりぐりうごかしまくるウホ。
動かすときには、放物線のちょうてんにちゅうもくするウホ。
二次関数のしきをしたにかくウホ。
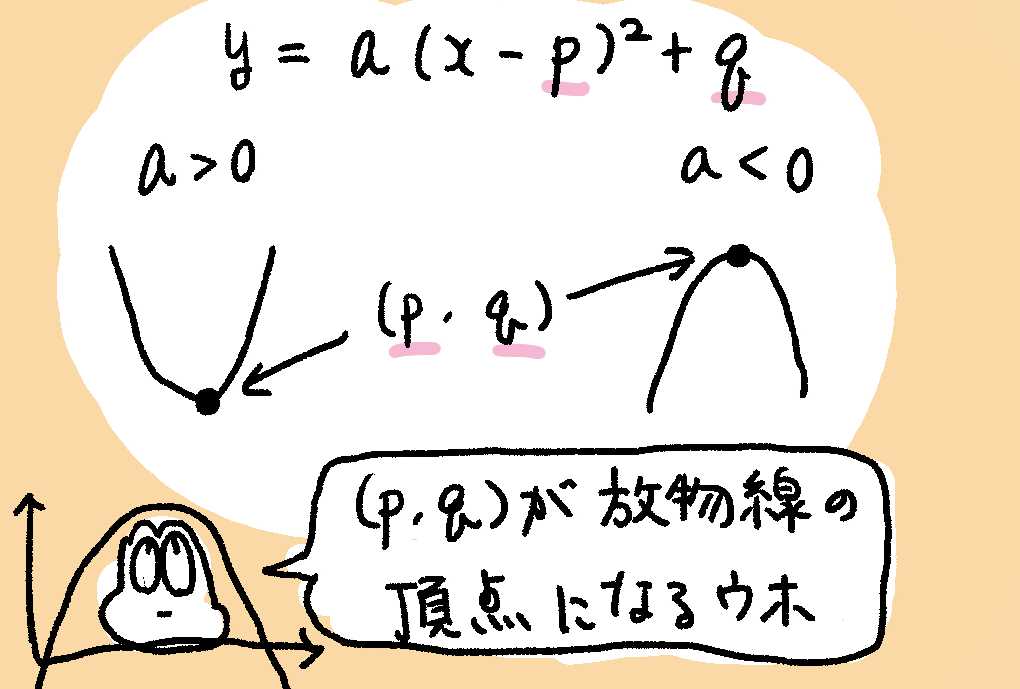
$y = a(x - p)^2 + q$
ちゅうがっこうまでは下みたいなかたちでならっていたはずウホ。
$y = ax^2$
ちゅうがっこうまでの式では、$a$が0より大きいと放物線は下にとんがった形で、0より小さいと上にとんがったかたちだったはずウホ。
高校では、これをはってんさせていくウホ。きほんてきには中学校までとおなじように、$a$が放物線のむきをきめるウホ。
そして、$p$とか$q$とかがこんかいのもんだいのポイントになるウホ。これは、($p$, $q$)が放物線の頂点になるということになるウホ。
…
きになるゴリラは、$x$にいろいろ数をいれてみてほしいウホ。たとえば、$a = 1$として、
$y = (x - p)^2 + q$
のときをかんがえるウホ。このとき、放物線はしたむきにとんがってることになるウホ。
たとえば、$x = p$のときには、$y = q$になるウホ。これが、したにとんがってる放物線の頂点(いちばんちいさいところ)になっていてほしいウホ。
おなじように、こんどは$x = 0$のときを考えるウホ。このときには、$y = p^2 + q$になるウホ。
$y = q$と$y = p^2 + q$をくらべると、$p^2$は正になるから($p$とか$q$とかは整数だとするウホ)、$y = q$のほうがちいさいことになるウホ。
めんどうだからしょうりゃくしちゃうけど、他の場合でも$x = p$のときが一番小さくなるウホ。このことから、$x = p, y = q$がほうぶつせんのちょうてんになることがわかったウホ。
…
さておき、もんだいのつづきをやってみるウホ。
このもんだいはシンプルで、頂点が(5, 25)になっていてほしいとかいてあるウホ。ようするに、$p = 5, q = 25$になるウホ。
このじてんで二次関数の式はつぎのようになるウホ。
$y = a(x - 5)^2 - 25$
つぎはなにをしりたいウホ?まだわかっていないもじには、$a$があるウホ。このaをしりたいウホ。
$a$をしるためには、xとyにかずをいれるウホ。さいわい、このグラフは原点をとおってほしいともんだいにかいてあるウホ。
だから、$x = 0, y = 0$を代入すると、
$0 = a(0 - 5)^2 + 25$
になって、せいりすると$a = -1$になるウホ。
よって、もとめたい二次関数の式は、
$y = -(x - 5)^2 + 25$
になるウホ!
こたえ:$y = -(x - 5)^2 + 25$
じぶんのあたまを数式であらわせると、なんだかせかいがひろがったようなきぶんになるウホ!そのうち、プログラムでじぶんのあたまをかかせるようにもしていきたいウホ。
ほかにも、もうちょっとリアルなかたちの曲線がかけるように、べんきょうをつづけていきたいウホ。