ゴリラと学ぶ「斜方投射」

ゴリのいる森🌲にニンゲン👩がやってきたウホ。ニンゲンはゴリに気がついていないみたいだけど、ゴリはきちんときがついているウホ。
ゴリとニンゲンは100 mくらいはなれているから、あいさつするにはちょっと遠いウホ。ゴリからニンゲンに、なにかあいさつがわりにプレゼントをあげることをしたいウホ。
ちょっとまえに、木の下の人間にクッキー💩を水平投射することをかんがえたウホ。にたようなかんじで、こんどは、ゴリも地面のうえからものをなげることをかんがえるウホ。
さっそく、もんだいとしてかんがえてみるウホ。
もんだい
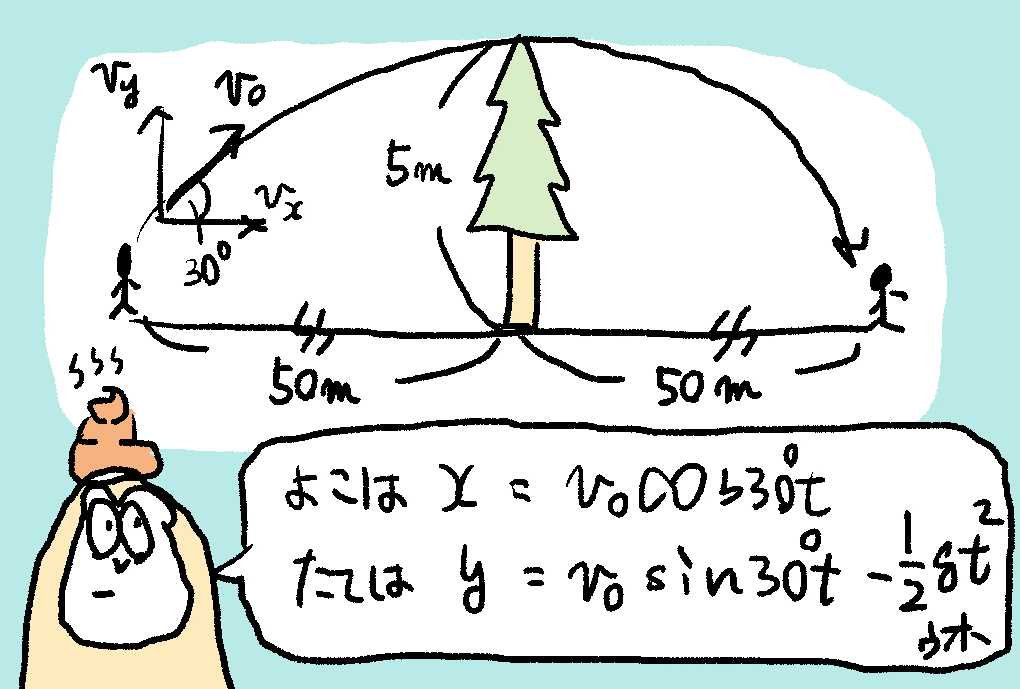
ゴリからニンゲンにたいして、らせんのカレーパン💩をなげるウホ。ゴリからニンゲンまでは100 m離れていて、放物線をえがくようになげるウホ。
とちゅう、ゴリとニンゲンのきょりのちょうど真ん中には、高さ4.5 mの木🌲があるウホ。いちおう、この木をじゅうぶんとびこえられるように、放物線のちょうてんがちょうど5 mになるようになげるウホ。
ここで、ゴリが30°の角度でなげるとき、どれくらいの速さ(初速度)でなげればいいウホ?
ただし、らせんのカレーパン💩の質量とか無視して、くうきていこうとか無視して、横には等速直線運動でうごいたりとか、なんかいろいろとすごくたんじゅんな方法で考えるウホ。
あと、こんかいゴリは地面すれすれのアンダースローでなげるものとするウホ。ようするにゴリのしんちょうはむしするウホ。そして、ニンゲンの身長も無視することにするウホ。
ひつようなら、つぎのすうじをつかっていいウホ。
- $g$(重力加速度) = おおざっぱに10とする
- $\rm{sin}30 = 0.50$
- $\rm{cos}30 = 0.87$
💩🌲🦍💩🌲🦍💩🌲🦍💩🌲🦍💩🌲🦍
こたえ
ゴリが、今度はニンゲンに対して斜方投射でものをなげるウホ!斜方投射は、ざっくりいうと山なりなきどう(放物線)をえがくなげかたウホ。
斜方投射の式をせいりしておくウホ。ニンゲンは、高校物理(物理基礎)でならっているとおもうウホ。
| 方向 | きょり | 速度 |
|---|---|---|
| よこ | $x = ν_0\rm{cos}θt$ | $ν_x = ν_0\rm{cos}θ$ |
| たて | $y = ν_0\rm{sin}θt - \frac{1}{2}gt^2$ | $ν_y = ν_0\rm{sin}θ - gt$ |
ここで、もじはつぎのようにおいたウホ。
| もじ | いみ |
|---|---|
| $x$ | よこほうこうのきょり |
| $y$ | たてほうこうのきょり |
| $ν_0$ | しょそくど |
| $θ$ | かくど |
| $t$ | 💩とぶじかん |
| $ν_x$ | よこほうこうの速度 |
| $ν_y$ | たてほうこうの速度 |
これをつかってけいさんしていくウホ。
まず、いきなりだけど問題をすこしよみかえるウホ。
とんでいくのは100 mではあるけど、このほうぶつせんは対称なかたちをとっているとかんがえるウホ。
つまり、半分の50 mでちょうど頂点にたっすることをかんがえるウホ。
そうすれば、残りの半分をかんがえなくても、もくひょうとして半分だけかんがえればいいことになるウホ。
そこで、「50 mじてんで、ちょうてんにたっしている」ことからかんがえるウホ。
まず、ちょうてんにたっしているということは、そのときのらせんのカレーパン💩は、みかけじょう上方向にはすすんでいないことになるウホ。よこほうこうにはじゅんちょうにすすんでいるけど、これから落下にはいることになるウホ。
ということは、たてほうこうの速度$ν_y = 0$であることを考えるウホ。
そうすると、うえの表で表した、たてほうこうの速度の式から、
$0 = ν_0\rm{sin}θ - gt$
とおけるウホ。さらに、$g = 10$,$\rm{sin}30 = 0.50 = \frac{1}{2}$から、
$0 = \frac{1}{2}ν_0 - 10t$
として、しきをへんけいすると、
$t = \frac{1}{20}ν_0$
になるウホ。
…
おなじように、よこほうこうについても考えるウホ。
よこほうこうには、100 mのはんぶんでいいから、50 mとばすことをかんがえるウホ。
そうすると、よこほうこうの距離の式から、
$50 = ν_0\rm{cos}θt$
で、$\rm{cos}θ$はけいさんがめんどくさそうだからそのままおいといて、しきへんけいすると、
$t = \frac{50}{ν_0\rm{cos}θ}$
になるウホ。
そして、さっきのたてほうこうのときにかんがえた$t$をつかうと、
$\frac{1}{20}ν_0 = \frac{50}{ν_0\rm{cos}θ}$
で、式をせいりすると、
$ν_0^2 = \frac{1000}{\rm{cos}θ}$
で、$\rm{cos}θ = \rm{cos}30° = 0.87$をだいにゅうしてけいさんすると、
$ν_0^2 ≒ 1149$
$ν_0 ≒ 34 (m/s) = 122 (km/h)$
になるウホ!げんみつにいうとちがうかもだけど、だいたい野球でピッチャーやるときくらいの強さでなげるといいかもしれないウホ。
こたえ: 34 m/s (122 km/h)
れいによって、まえにこんがりチョコクッキー💩をあげたときとおなじようなはんのうをされたウホ。かるい悲鳴をあげたけど、たべられることをつたえたらもってかえってくれたウホ。
ニンゲン👫とゴリラ🦍のゆうこう✌のために、これからもどんどんこうりゅうをふかめていきたいウホ。