ゴリラと学ぶ「水平投射」

作成: 2020-01-21 | 更新: 2020-01-21

gori0000025

ゴリはいつもどおり、木🌲のてっぺんでやすんでいたウホ。木のてっぺんにいると、あたりが見渡せて👀きぶんがいいし、あやしい👿ものも見つけやすいウホ。
すると、木の下にニンゲン👦がたっていたウホ。たぶん、このへんをさんぽ👣していて、ちょっときゅうけいするつもりなんだと思うウホ。

ふよういにちかづいてくるニンゲン👦には、こんがりチョコクッキー💩をなげるウホ。かんげいのしるしと、ちょっとしたいたずらウホ。

もんだい

木のふきんで立ち止まっているニンゲンは、木の位置から14 mのところにいるウホ。

このニンゲンに、ゴリが上から水平投射して、下のニンゲンにこんがりチョコクッキー💩をおみまいするとき、どれくらいの速度で投げればいいウホ？

ただし、以下の条件をつけるウホ。

つぎのあたいをつかってもいいウホ。

👦🦍👦🦍👦🦍👦🦍👦🦍

ゴリはこれから、水平投射をすることになるウホ。なにかものをなげるばあいじゃないけど、ゴリラが自由落下（水平投射）する場合🦍については、まえにもうかんがえていたウホ。

また、ゴリ🦍からニンゲン👦までの距離を角度📐をつかってしるのは、まえに木の上からゴリラまでの距離をはかるやつでかんがえていたウホ。

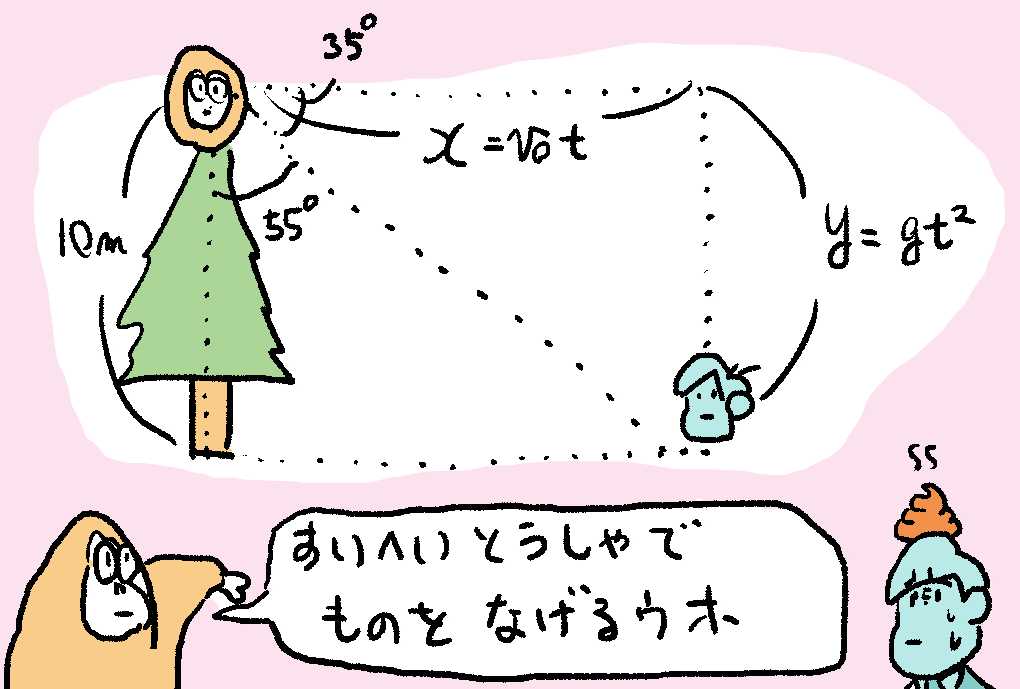
gori0000025-2

ゴリからニンゲンまでの角度は35°ウホ。いいかえると、木からゴリ-ニンゲン目線までの角度は、90° - 35° = 55°になるウホ。
ここから、

$\frac{木からニンゲンまでの🌲👦距離（m）}{木からゴリの目線までの🌲👀高さ（m）}$ $= tan55°$

になるウホ。木からゴリの目線までの距離🌲👀は10 mだったから、
$tan55° ≒ 1.40$（ほんとは1.428…だけどざっくり）をつかって、木からニンゲンまでの距離🌲👦は14 mになるウホ。

つぎに、落下するまでの時間を計算するウホ。らっかは、くうきていこうの影響をうけないとしているから、自由落下だとかんがえるウホ。

自由落下の式は、$y = \frac{1}{2}gt^2$（$y$ = らっかきょり($m$)、$g$ = 重力加速度($m/s^2$)、$t$ = らっかじかん($s$)）だったウホ。これをつかうと、

ゴリのめせん👀から地面までの距離 = ゴリの目線👀からニンゲン👦まで落ちる距離

$= 10 m = \frac{1}{2} × 10 m/s^2 × t^2$

だから、$t = \sqrt{2} ≒ 1.4 (s)$になるウホ。

あとは、等速直線運動する場合をかんがえるウホ。条件から、ものをよこになげたときは、

$x = ν_0 t$

$x$ = いどうきょり（$m$）、$ν_0$ = $しょそくど（$m/s$）$、$t$ = いどうじかん（$s$）

とするウホ。いま、いどうきょり（14 $m$）といどうじかん（1.4 $s$）はわかっているから、
あとはしょそくどをけいさんして、10 $m/s$となるウホ。これは、時速だと36 $km/h$だから、ゆっくりなげるウホ！

こたえ：10 $m/s$（時速だと36 $km/h$）

こんがりチョコクッキー💩をくらったニンゲン👦は、さいしょは苦虫をかみつぶしたような顔をしたウホ。でも、それがただのクッキーだとわかると、ゴリに手をふって👋おれいをいって、かえっていったウホ。なにとかんちがいしたかはしらないけど、おいしいクッキー💩をぜひあじわってほしい😊ウホ。