ゴリラと学ぶ「一次関数」動く点と面積編

ゴリたちゴリラは、ナワバリについて日々いしきしながら生活しているウホ。まえにも、木の上からナワバリにはいってくるゴリラを見たりとか、ほかのゴリラとのぼる木がかぶっちゃう確率についてかんがえたりしたウホ。ニンゲン👫も、土地をナワバリとして生活しているから、なわばりについて考えていることは多いと思うウホ。
今回は、ナワバリの面積について考えていきたいウホ。とくに、動いているゴリと木々でできるナワバリについてかんがえていくウホ。これをかんがえると、いままで面積が固定されていたナワバリの問題について、面積が変わる時のことも考えることができるウホ!
もんだい
ジャングルの中で、木🌲が正方形のかたちになっているウホ。
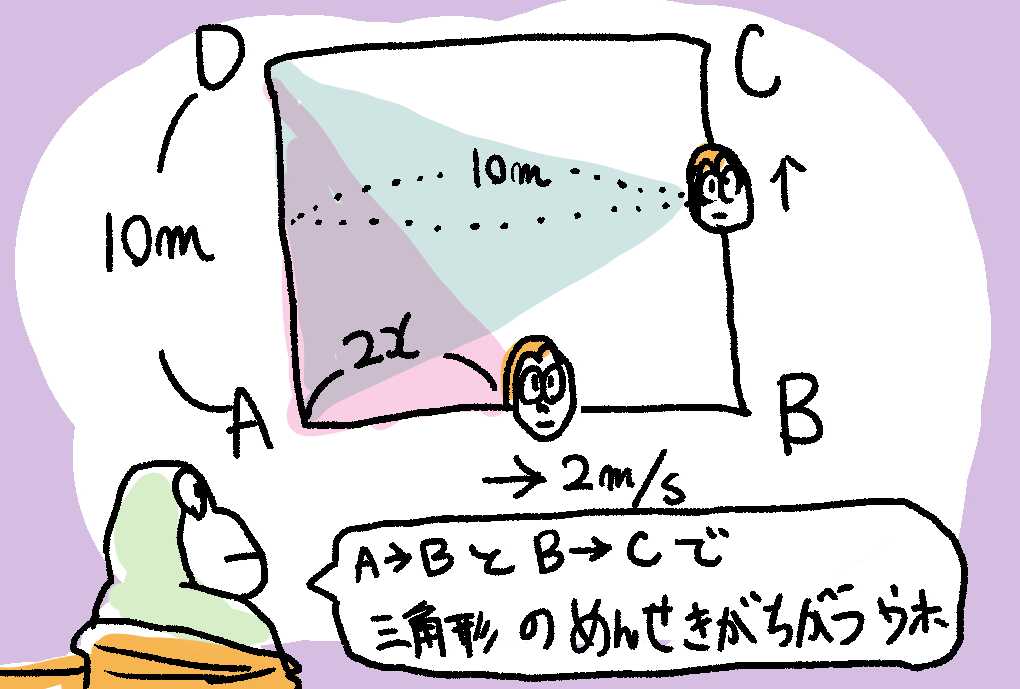
この正方形は、左下がA、右下がB、右上がC, 左上がDと区別できるウホ。
いま、ゴリが木Aからスタートして、木Aから木B、木Bから木Cまで、毎秒2 m(2 m/s)でうごくとするウホ。
そして、ゴリは木Aと木Dからロープ🧶をピンとのばして、木A-木D-ゴリラでできる三角形の面積をナワバリだということにするウホ。
このとき、次の場合について、ゴリがつくるナワバリの面積を計算してほしいウホ。また、それぞれ何秒から何秒までのことなのかを答えてほしいウホ。
面積が数字ではっきりと決まらないときは、秒数を$x$としてこたえてほしいウホ。
- ゴリがAからBまでいどうするとき
- ゴリがBからCまでいどうするとき
🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲
こたえ
さくさくいくウホ!この問題は、ニンゲンが中学数学でならう、一次関数でかんがえるウホ。
まず、スタート直後をかんがえるウホ。ゴリが持っているナワバリは、木Aから木Dまでのちょくせんだとかんがえると、じっしつゼロになるウホ。だから、ゴリの持っているナワバリは一番小さくて0になるウホ。
つぎに、それぞれ問題の中でしじされていることについてかんがえていくウホ。
…
- ゴリがAからBまでいどうするとき
ゴリがAからBまで移動するとき、A-D-ゴリの三角形は、底辺(高さとかんがえてもいいウホ)が時間とともにのびていくウホ。具体的には、毎秒2 m(2 m/s)だから、一辺のながさが10 mということで、5秒後までに0, 2, 4, 6, 8, 10と底辺がのびていくウホ。
たとえば、ゴリがしゅっぱつして1秒後、つまり2 mすすんだときには、三角形の面積はどうなるウホ?
このときには、三角形の面積の公式(面積 = 底辺 × 高さ ÷ 2)をつかうと、高さは木A - 木Dのきょり(つまり10 m)として、
$面積 = 2 × 10 ÷ 2 = 10 m^2$
になるウホ。
つまり、秒を$x$とおくなら、
$面積 = 2x × 10 ÷ 2 = 10 m^2$
で、10 ÷ 2 = 5してととのえると、
$面積 = 10x m^2$
になるウホ!
すなわち、ゴリがAからBまでいどうするときは、0から5秒後までで、$面積 = 10x m^2$になるウホ!
いちばんおおきくて、面積は$x = 5$として$50 m^2$になるウホ。
…
- ゴリがBからCまでいどうするとき
つぎのもんだいは、BからCまでいどうするときについての問題だウホ。
このとき、実は木Aから木Dまでの距離を三角形の底辺とすると、高さが一定でうごくことになるウホ。
つまり、高さが正方形の一辺の長さ(10 m)とおなじになるから、面積は$50 m^2$になるウホ!
ちなみに、すすんでいるゴリの速度はおなじだから、今度は5から10秒までいどうすることになるウホ。
すなわち、ゴリがBからCまでいどうするときは、5から10秒後までで、$面積 = 50 m^2$になるウホ!
いちばんおおきくて、というかずっと面積はおなじで、$50 m^2$になるウホ。
こたえ:
- ゴリがAからBまでいどうするときは、0から5秒後までで、$面積 = 10x m^2$になる($0 から 50 m^2$)。
- ゴリがBからCまでいどうするときは、5から10秒後までで、$面積 = 50 m^2$になる。
さっくりと、ゴリラ🦍を動く点とした面積の変化についてかんがえられたウホ。ゴリたちは木🌲をナワバリの基準にしているけど、もしなにか動いているものをナワバリの基準にしたいときは、次からはこのことを思い出しながら考えていきたいウホ!