ゴリラと学ぶ「二進数」足し算・引き算編
いぜんにゴリ進数🦍についてきめたり、ゴリ進数をPythonでデコード(utf-8)したり🐍したウホ。ゴリ進数はじっしつ二進数だから、二進数にできることはほとんどできるウホ。
ゴリ進数はゴリラ界隈にもだいぶん浸透してきた(ゴリ的には)ウホ。そうこうしていると、ゴリ進数をつかってバナナ🍌のかいものの計画をたてているゴリラ🦍がいたウホ。ゴリもお買い物のお手伝いになればと、計算をいっしょにやってみたウホ。
もんだい
以降の数字は、みんなゴリ進数であらわしているウホ。
あるゴリラAが、ゴリ進数でバナナ🍌を買うときの計算したウホ。
そのゴリラAは、ウホウホウ本のバナナが欲しかったウホ。これは、ゴリラAのかぞくウ人当たりでウウウ本というけいさんになるウホ。
でも、やっぱりウ人分はいらなくなったから、ウホウホウ本からウウウ本のバナナをひいたウホ。
さらに、ウ人分をひいたものの、やっぱりあとウホ人分が追加でほしくなったから、そのぶんだけバナナをついかでかうことにしたウホ。
これについて、次の問題に答えてほしいウホ。
- ゴリラAが最初に買おうとしていた、ウホウホウ本からウウウ本を引くと、バナナは何本になるウホ?
- 最初のゴリラAの家族ウ人あたりでウウウ本といったとき、ゴリラAの家族は何人いるウホ?
- ゴリラAは、ついかで何本のバナナを買うことになったウホ?
- けっきょく、ゴリラAは合計で何本のバナナを買うことになったウホ?
ヒント:ゴリラは「ウホ」というと、人差し指と中指をたててこっちにむけたウホ。これが「ウホ」があらわすことらしいウホ。
🦍🍌🦍🍌🦍🍌🦍🍌🦍🍌🦍🍌
こたえ
もうらてきに、四則演算(足し算、引き算、掛け算、割り算)をぜんぶやることになったウホ。順番に答えを見ていくウホ。
けっきょくは、ゴリ進数は二進数の文字を変えただけだから、二進数の計算になれているゴリラは、そのまま二進数のつもりで計算してほしいウホ。二進数の計算になれていないゴリラは、いちど十進数になおしてから計算するとやりやすいとおもうウホ。
十進数も二進数も、桁のあがりさがりについてはおなじような感覚でけいさんできるウホ。
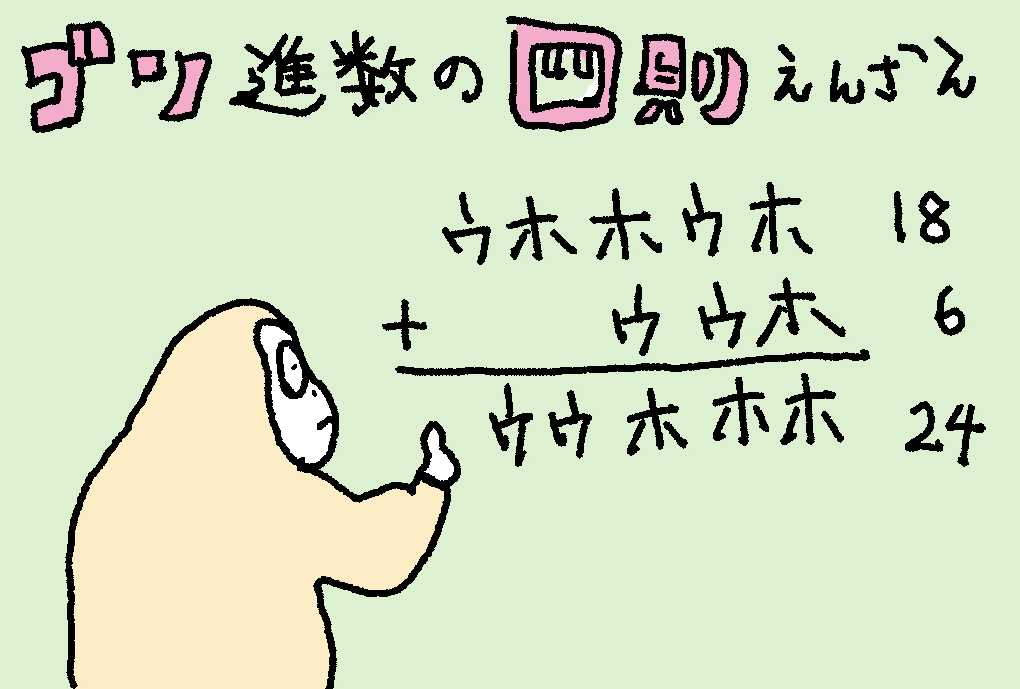
…
- ゴリラAが最初に買おうとしていた、ウホウホウ本からウウウ本を引くと、バナナは何本になるウホ?
「ウホウホウ」から「ウウウ」を引くウホ。これは、一桁目が「ウ」から「ウ」を引くので「ホ」になって、二桁目は「ホ」引く「ウ」だけど、これは引けないから、三桁目の「ウ」を「ホ」にしたうえで、二桁目をウにするウホ。また、三桁目の「ホ」からも「ウ」は引けなくて、四桁目の「ホ」から「ウ」をもらうことができないから、五桁目の「ウ」を「ホ」にして、四桁目を「ウ」、三桁目を「ウ」にするウホ。
そうすると、答えはウウウホになるウホ。
十進数(二進数)でいうと、21(10101)引く7(111)が14(1110)になるウホ。
…
- 最初のゴリラAの家族ウ人あたりでウウウ本といったとき、ゴリラAの家族は何人いるウホ?
ゴリラAの家族を変数(🍌)であらわすウホ。これは、ニンゲンが$x$とおくのと同じように、かわりにバナナをおいているウホ。
ウホウホウ本のバナナは、ゴリラの家族がウ人当たりでウウウ本だから、これを式で表すとつぎのようになるウホ。
$\frac{ウホウホウ}{🍌} = ウウウ$
これをせいりすると、
$🍌 = \frac{ウホウホウ}{ウウウ}$
になるウホ。
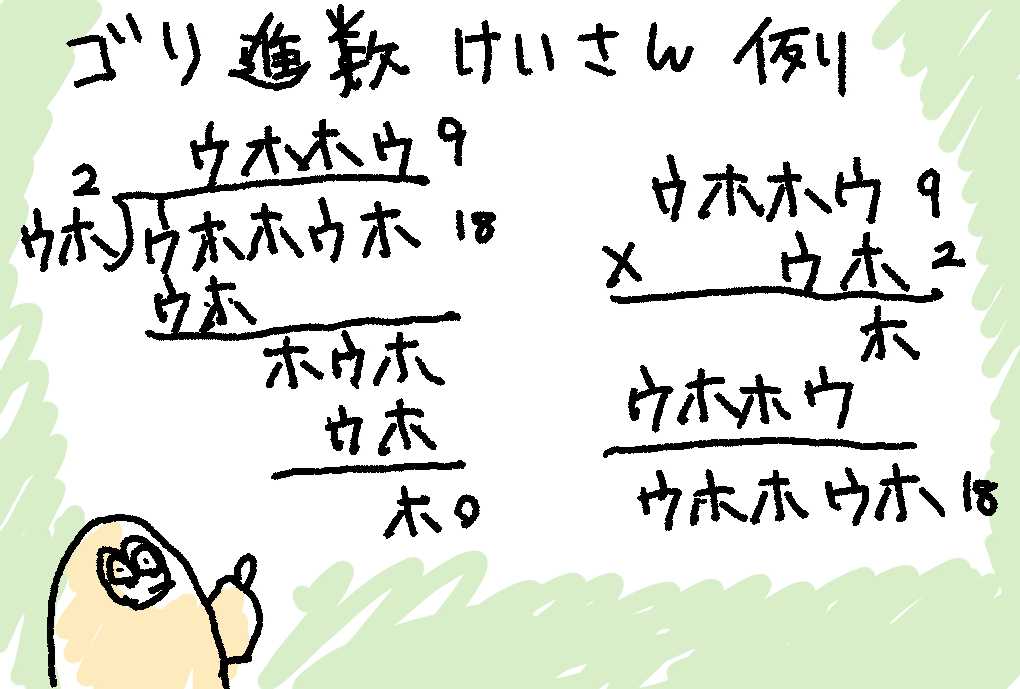
割り算の計算のときは、ちょっとふくざつだけど、引き算のときとおなじようにけいさんするウホ。そうすると、ウウであまりはホになるから、
$🍌 = ウウ$
になるウホ。このことから、ゴリラAの家族はウウ人ということになるウホ。
ちなみに、十進数(二進数)では、21(10101)本のバナナが1(1)人あたり7(111)本で、ゴリラの家族は3(11)人ということになるウホ。
…
- ゴリラAは、ついかで何本のバナナを買うことになったウホ?
ゴリラAは、ウウ人からウ人のゴリラを引いて、ウホ人のゴリラのためにバナナを買うつもりだったウホ。
でも、やっぱり、ここからさらにウホ人のゴリラ分だけバナナを追加することにしたウホ。
そうすると、さっきウ人当たりのバナナの本数はウウウ本だといっていたから、ウウウ × ウホをすることになるウホ。
掛け算の計算も、いままでとおなじウホ。二進数、もといゴリ進数の掛け算はいくぶん簡単で、掛け算するじてんでは桁上がりを意識しないですむウホ。なんといっても、ウかけるウはウだし、ホになにをかけてもホになるウホ。そのあとに足し算をするフェーズでは桁上がりはいしきしないといけないウホ。
ということで、ウウウ × ウホはウウウホになるウホ。十進数(二進数)では、7(111) × 2(10)は14(1110)になるウホ。
…
- けっきょく、ゴリラAは合計で何本のバナナを買うことになったウホ?
ゴリラAは、けっきょく合計で(ウウ - ウ) + ウホ = ウホホ人分のバナナを買うことになるウホ。ウ人当たりのバナナはウウウ本だったから、ウウウ × ウホホをすることになるウホ。計算すると、ウウウホホ本のバナナを買うことになったウホ。
ということで、こたえはウウウホホ本になるウホ。十進数(二進数)では、7(111) × 4(100)は28(11110)になるウホ。
こたえ:
- ウウウホ
- ウウ
- ウウウホ
- ウウウホホ
ゴリラ🦍はまんぞくしてお買い物ができたみたいだウホ。いきようようとウウウホホ本のバナナを買って帰っていったウホ。
そんな様子を見ていると、ゴリもおなかがすいてきたウホ。ゴリもウホホ本くらいバナナ🍌をかって💰かえろうとおもうウホ。
そういえばだけど、ゴリ進数をつかうと、十進数も「ウホウホ進数」、二進数も「ウホ進数」ということができるウホ。今後気が向いたらそういう言い方をしてみようとおもうウホ。