ゴリラと学ぶ「比例と反比例」
これまでにこのサイトでいろいろとゴリラ🦍についての問題をとりあげているけど、どれが比例でどれが反比例かの分類はしてなかったウホ。
言葉のおさらいをしておくと、たとえば$y$と$x$っていう変数があったときに、
- 関数 …$x$がきまれば$y$もただひとつ決まる
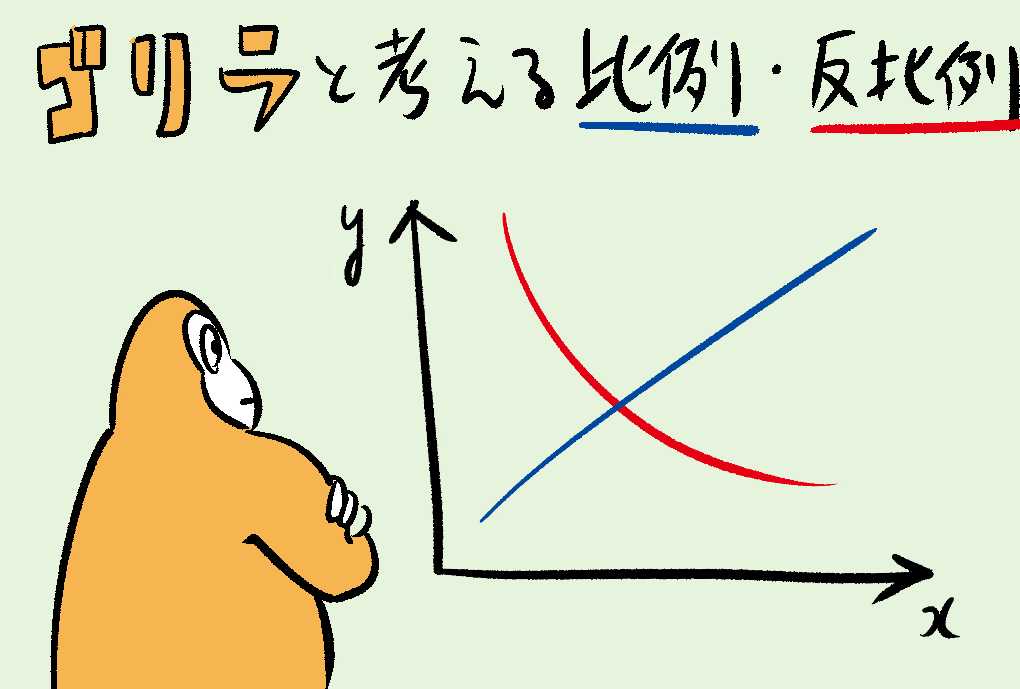
- 比例 …$x$が増えると$y$もふえるような、$y = ax$みたいな関係($a$は比例定数)
- 反比例 …$x$が増えると$y$はへるような、$y = \frac{1}{x}$みたいな関係
だったウホ。ゴリ的なざっくりせつめいだから数学的に正しくないかもだけど、だいたいこんな感じウホ。
ニンゲン👫もいろいろな問題をすうがくてきに考えることがあると思うけど、そのときには比例だったり反比例だったりを意識することがあると思うウホ。
今回は頭の体操として、いろいろな問題について比例か反比例かを分類してみるウホ。
もんだい
つぎのもんだいについて式としてあらわしてみてほしいウホ。それが比例か反比例か、どちらでもないかを分類してほしいウホ。
そのとき、できれば式でもあらわしてほしいウホ。
- ゴリラが時速$x$ kmで走ると、2時間で$y$ kmすすむ。
- ゴリラがバナナを$x$等分すると、15 cmのバナナが$y$ cmに分けられる。
- あるゴリラが一日にバナナを$x$束食べたら体重が1 kgずつ増えていき、もとあった150 kgが$y$ kgになった。
- ゴリラのナワバリは一辺が$x$メートルの正方形で、面積は$y$平方メートルになる。
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
さっそく一個ずつみていくウホ!
…
- ゴリラが時速$x$ kmで走ると、2時間で$y$ kmすすむ。
これは「道のり = 速さ × 時間」であらわせるウホ!さっそくあらわしてみると、
$y = 2x$
になるウホ。そして、$x$の値に対して$y$がただ一つ決まるから、これは比例になるウホ!
…
- ゴリラがバナナを$x$等分すると、15 cmのバナナが$y$ cmに分けられる。
バナナが等分されるたびに、分けられたバナナはどんどん小さく、数は多くなっていくウホ。そうすると、式としては次のようになるウホ。
$y = \frac{15}{x}$
これは反比例の式になるウホ。
…
- あるゴリラが一日にバナナを$x$束食べたら体重が1 kgずつ増えていき、もとあった150 kgが$y$ kgになった。
もともと150 kgあった体重が、一束たべるたびに1 kgずつ増えていったとするウホ。そうすると、体重$y$は次のようになるウホ。
$y = 150 + x$
$x$の前についている、比例定数としての1は省略したウホ。
そしてこれが比例の関係にあるかというと、これは一次関数となるウホ。ややこしいけど、一次関数は比例の関係とはいえないウホ。
Wikipediaだけど、比例とは「変数を用いて書かれる二つの量に対し一方が他方の定数倍であるような関係」(Wikipedia - 比例)とかいてあるウホ。ようするに、$y = ax$みたいな関係で、$y = ax + b$だと$b$がはいってくるぶん単なる比例の関係じゃなくなっちゃうウホ。
だから、この問題は比例でも反比例でもないウホ。しいていえば一次関数の問題ウホ。さらに、これが一般的なゴリラにあてはまるかというと、その一人のゴリラがたまたまそういう体重の増え方をしたかもしれないから、そもそもの問題としてなんともいえないというほかないウホ。
…
- ゴリラのナワバリは一辺が$x$メートルの正方形で、面積は$y$平方メートルになる。
これを式で表すと次のようになるウホ。
$y = x^2$
これは、$x$の二乗がでてきているウホ。中学一年生のニンゲンはまだならってないかもだけど、二次関数としてあらわされるウホ。
これは比例でも反比例でもないウホ。
こたえ: 上記の通り
よのなかのいろいろな問題は式であらわせることがあるウホ。でも、ゴリもよくこんがらがるけど、比例なのか反比例なのか、それとも別の関数なのかはけっこうぐちゃぐちゃになっちゃうこともあるウホ。
みんなはある問題にあたったときには、れいせいにそれがどういう関係なのかを判断していってほしいウホ。