ゴリラと学ぶ「場合の数」となりあう編

ゴリたちゴリラ🦍はたびたびナワバリをうばいあう争いをするウホ。いきなりだけど今回もナワバリの話ウホ。五人のゴリラがいて、ナワバリをじゃんけんで取り合おうとしているウホ。ゴリはそれを横目に見ながら、ナワバリのわかれかたも気になるけど、ナワバリの数にはどれくらいのパターンがあるかのほうが気になっちゃったウホ。
さっそく計算してみることにしたウホ。
もんだい
ある5人のゴリラ🦍たちが、5つのナワバリの分け方を考えているウホ。
このナワバリは、5つが接して隣り合っているウホ。
いま、ゴリラたちがじゃんけんして、勝ったゴリラが好きなナワバリを選べるとするウホ。
このとき、つぎのじょうけんにしたがうとするウホ。
- ゴリラがもてるナワバリは一つだけじゃなくて、2つ以上もつこともできるウホ。
- あるナワバリをとったら、となりあうナワバリはとることができないウホ。
- かわいそうなゴリラは一つもナワバリをもつことができないこともあるウホ。
それでは、5人のゴリラが、5つのナワバリをわけるときの場合の数は、何通りになるウホ?
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
ニンゲンが中学校でならう、「場合の数」をつかうウホ!場合の数は、まえにも「二匹のゴリラに挟まれる場合の数ウホ」でやったウホ。
真ん中からとりはじめたりするとややこしいから、左からとることにするウホ。
いま、ゴリラは5人いるウホ。これらをゴリラ(A, B, C, D, E)とわけることにするウホ。
A, B, C, D, Eのうち、まずはAが左端のナワバリを持つと考えるウホ。
そうすると、次のナワバリには、となりあうナワバリには同じゴリラはとれないから、A以外のB, C, D, Eのどれかが入ることになるウホ。
で、仮にBが入るとすると、おなじように次のナワバリには、B以外のA, C, D, Eが入ることができるウホ。
その次にまたAが入ったとすると、B, C, D, Eが入るウホ。そのまた次に、またBが入ったらA, C, D, Eが入るウホ。
これで、最後の5つ目のナワバリまで入ったことになるウホ。
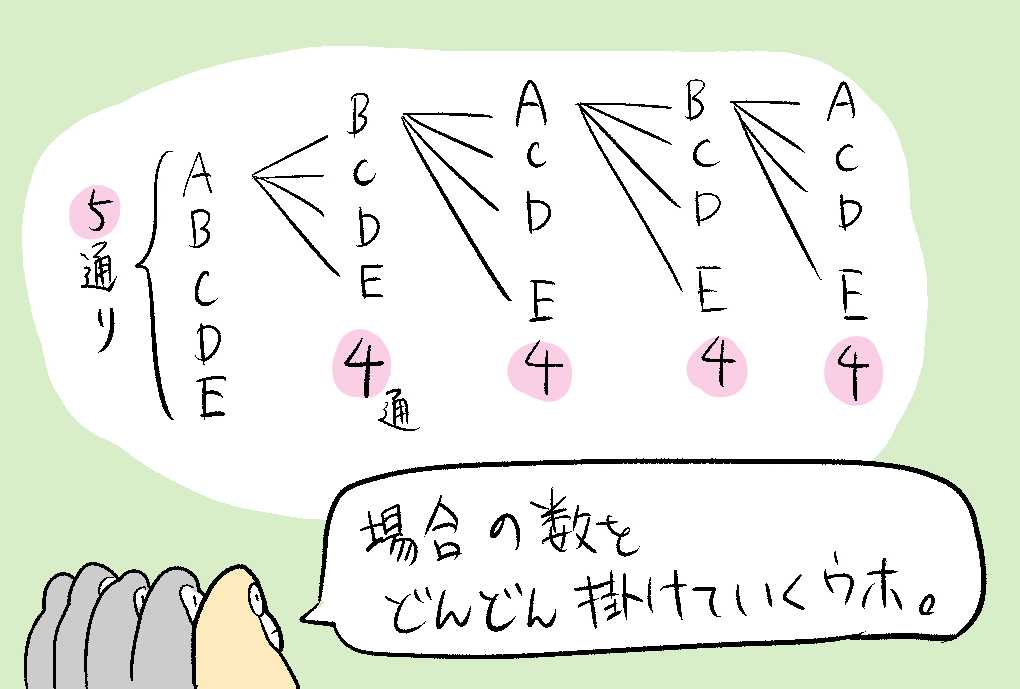
これをまとめると、最初には5通りのゴリラがはいりうるウホ。次からは4, 4, 4, 4通りと続くウホ。
このことから、場合の数としては、
5 × 4 × 4 × 4 × 4 = 1280通りということになるウホ!
こたえ: 1280通り
ゴリラたちは真剣にじゃんけんをして、ナワバリをとりあったウホ。そうすると、ゴリラAが3回勝って、ナワバリを1個ずつとびとびで計3個とることが出来たウホ!
ゴリラAはじゃんけんがすごいつよいウホ!ゴリが感心していると、結果に不満を持ったほかのゴリラたちとケンカになっちゃったウホ。
これじゃ公平に決めた意味がないウホ!ゴリはあきれかえりながら、おうちに帰ったウホ。