ゴリラと学ぶ「地球の円周」計算編

ゴリたちゴリラがナワバリのきのうえからみる地平線は、どこまでもはてしなくつづいているように見えるウホ。いったい地球のおおきさはどれくらいなのか、それをゴリたちゴリラがしるほうほうはあるのか、気になってきたウホ。
まえにゴリが、ゴリラの木からみえるナワバリのはんいを計算したりしたように、ゴリラたちもちきゅう🌍というものをゆうこうにかつようしていきたいウホ。そのためには、ちきゅうとはなにか、サイズや性質をいろいろとしらべていく必要があるウホ!
こんかいは、ほぼほぼゴリラ🦍だけをつかって地球の円周をはかるほうほうを考えてみるウホ。
もんだい
ゴリたちゴリラ🦍は、ゴリラだけをつかって地球の円周をしるためのほうほうを計画したウホ。
いまのところで、わかっているじょうけんは次の通りだとするウホ。
- ゴリラのしんちょうは、へいきんで1.6 mだとするウホ。
- ゴリたちの住んでいるジャングル(点A)では、正午に太陽がちょうど真上にくるウホ。
- 別のはなれている場所(点B)では、おなじじかん(正午)、木と太陽がなす角度はだいたい7.2°だとわかっているウホ。
- 地球は(ほんとは楕円だけど)まんまるな球だとしているウホ。
で、ほんとうは地球の円周をしるのがもくてきなんだけど、ここでは地球の円周を40000 kmだということにしちゃうウホ。
なぜかというと、考えてほしいのは、さまざまな長さはすべてゴリラをならべてはかるとして、いったい何匹のゴリラが必要かかんがえてほしいからそうしたウホ。
地球の円周をはかるには、身長1.6 mのゴリラを何人ならべるひつようがあるウホ?
🌍🌍🌍🌍🌍🌍🌍🌍🌍🌍🌍
かいとうあん
こんかいのもんだいぶんはちょっと遠回しないいかたになっちゃったから、わかりづらいところがあったらかんべんしてほしいウホ。いろいろ答え方はあるとおもうから、いちおうのこっちがきたいしているかいとうあんを書くウホ。
かつてニンゲンのうちのひとり、エラトステネスが紀元前3世紀くらいに測定したほうほう(wikipedia-英語版)をマネするウホ!
このほうほうでは、つぎのほうほうで地球の半径をしらべたウホ。
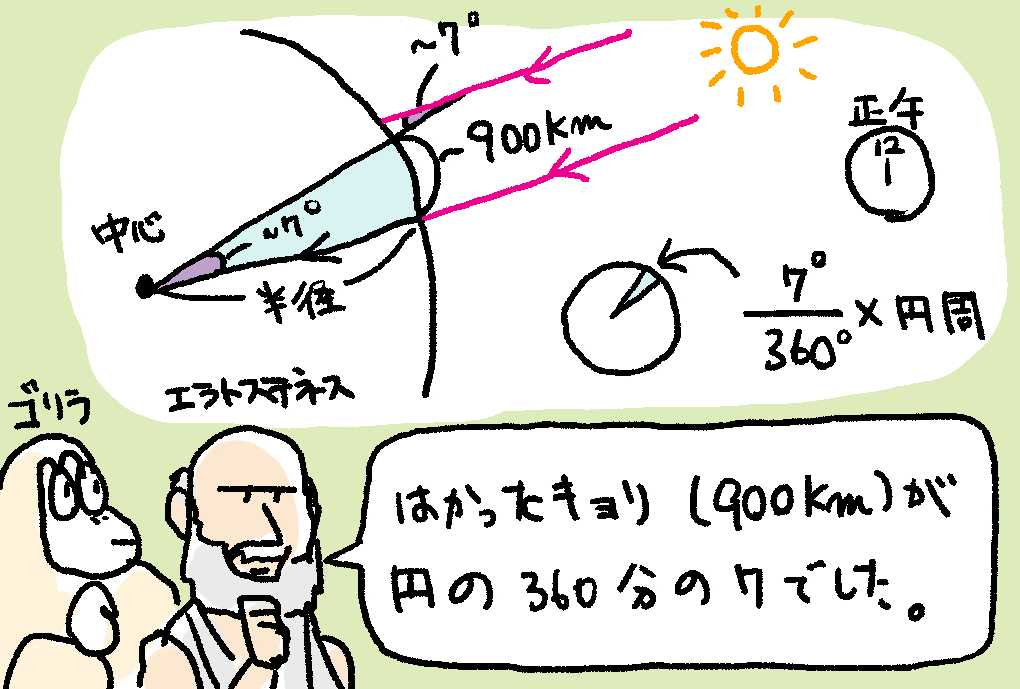
- シエネ(点A)からアレクサンドリア(点B)の距離がだいたい900 kmだとする。
- 太陽から地球には、光が平行に降り注いでいるとする。
- 点Aにある井戸は、赤道直下にあって光が垂直に入るから、その時(正午)をねらう。
- 点Bに、同じ時間(正午)に立てた棒では、角度とかげのなす角が約7°だった。
- 地球は球で、一周360°だということはしっていたから、900 kmというのは地球の全周の$\frac{7}{360}$だとわかった。
- ぎゃくにいえば、$\frac{360}{7} × 900$で地球の円周がでる。
これをおうようしてもとめられそうウホ!
…
さっそくけいさんしていくウホ。
うえのエラトステネスさんがやった方法では、シエネとアレクサンドリアのきょりが900 kmだということはわかっていたウホ。
じつはゴリがしりたかったのはその距離ウホ!その距離をはかるために、身長1.6 mのゴリラが何人必要なのかをけいさんしたかったウホ。
さておき、おなじようにけいさんしていくウホ。正午のときの点Bの角度は7.2°、地球が360°として、地球の円周が40000 kmだということにしているから、
$点Aから点Bまでの距離 = 40000 × \frac{7.2}{360} = 800 km = 800000 m$
エラトステネスさんのやつ(900 km)とはちょっと距離がちがうけど、遠からずもまあまあな数がでたウホ。
そして、これを身長1.6 m で割ることで、ひつようなゴリラの数がでてくるウホ!
$800000 / 1.6 = 500000$
50万人のゴリラがひつようになったウホ!これは、だいたい江東区の人口とおなじくらいのゴリラ(wikipedia)がひつようになるウホ。
こたえ: たんじゅんにならべるばあい、50万人のゴリラがひつよう
でも、リアルなゴリラは、ニシゴリラとヒガシゴリラでだいたい10~20万人1で、渋谷区の人口(wikipedia)よりもちょっとすくないウホ。とうてい足りないウホ!
リアルなゴリラをならべて地球の円周をはかるには、もっとふえるひつようがあるウホ。というか、それをいっちゃうとおしまいだけど、ふつうにロープか何かで工夫して距離をそくていするほうがはやいウホ。いっちゃったから今回はこれでおしまいウホ。