ゴリラと学ぶ「単位格子」原子の数編

ほうせき💎はパワーストーンとして、ふしぎなちからがあるとされているウホ。ニンゲン以外のいきもので、カラスとかもきらきらしたものがすきでよくあつめているウホ。ゴリも、ゴリラオリジナルの結晶なんていうのがあったら、すごいゴリラパワーをひめられそうウホ。
こんかいは、ゴリラパワーストーン🦍💎を考える準備として、ゴリラの結晶について考えていきたいウホ。
もんだい
ゴリライト💎という結晶を仮定するウホ。このゴリライトは、ゴリラパワーがぎゅうぎゅう詰めになってできているとするウホ。いこうはゴリラ1人 = ゴリラパワー 1人分 = 原子一個分として仮定するウホ。
いま、ゴリライトAとゴリライトBがあって、それぞれ次のような結晶構造をとるとするウホ。
- ゴリライトA…体心立方格子
- ゴリライトB…面心立方格子
単位格子(たんいこうし:ひとつのけっしょうのなかでいちばん小さくできる構造)にふくまれるゴリラの数は、どれくらいになるウホ?
💎💎💎💎💎💎💎💎💎💎💎💎💎
こたえ
このもんだいは、ニンゲンが高校化学でならう結晶の問題をあてはめるウホ。
体心立方格子と面心立方格子は、それぞれ次のようになるウホ。
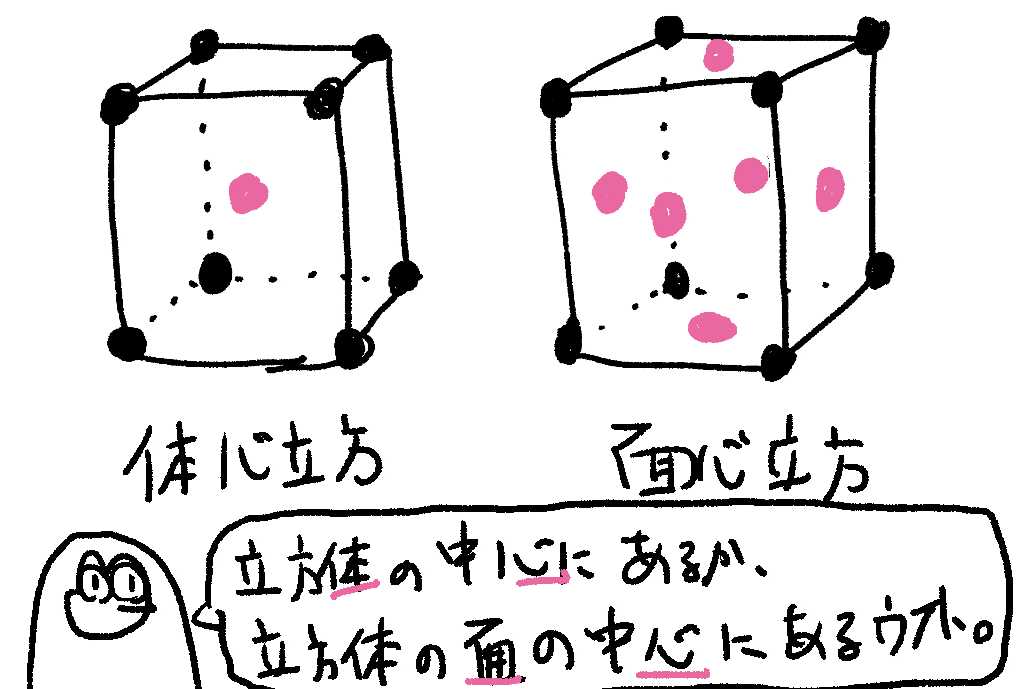
このときの、それぞれの単位格子、つまり立方体の中に、どれくらいゴリラがいるか(ゴリラパワーが含まれているか)をかんがえるウホ。
…
たんじゅんな考え方でもとめるウホ!まずは体心立方格子について考えるウホ。
ゴリライトA、つまり体心立方ゴリライトは、立方体の8このカドにゴリラがいて、あとは立方体のど真ん中にもゴリラがいる構造ウホ。
ということは、とりあえずど真ん中のゴリラ一人分は確定ウホ。
さらに、体心立方ゴリライトの8カドに8人だから、ゴリラはぜんぶで9人…としたいところだけど、じっさいにはちがうウホ。
単位格子が、この立方体の内側にあるゴリラにだけちゅうもくするなら、8つのカドのゴリラは、それぞれ上半身のいちぶだったり、下半身のいちぶだけが立方体にはいっているといえてしまうウホ。
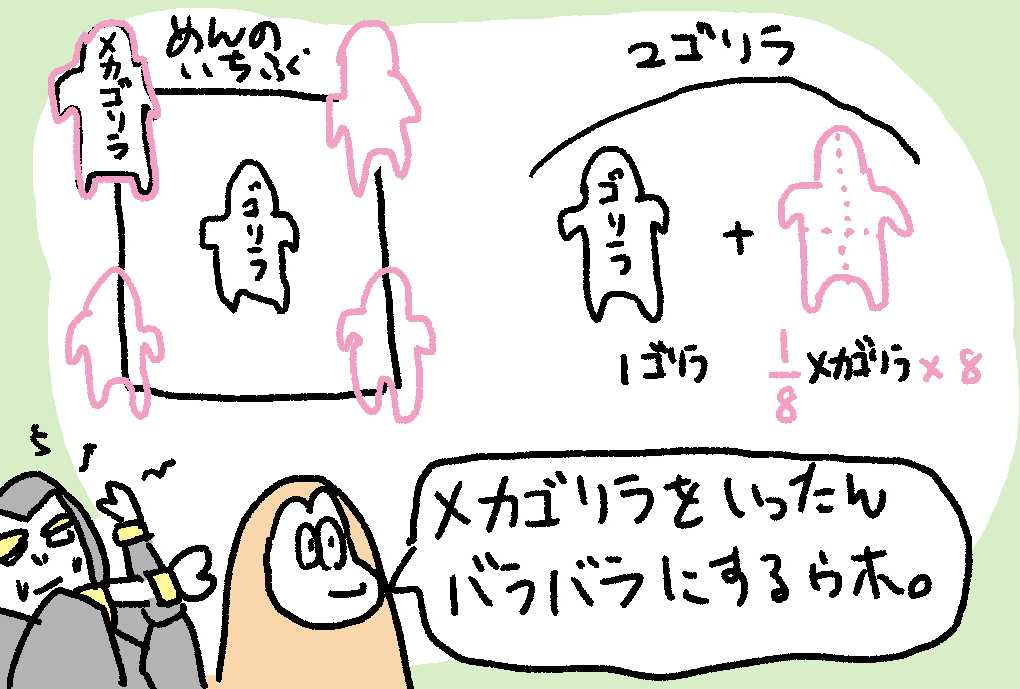
それじゃ話がややこしくなるから、ここでメカゴリラを導入するウホ!メカゴリラは分解することができるウホ。だから、立方体のかさなっている所でメカゴリラをばらばらにするウホ。
こうすることで、メカゴリラは一つのカドにつき、八等分されることになるウホ。
あとは、方体のなかにあるメカゴリラのパーツを集めることで、きちんと一体のメカゴリラになることができるウホ!
つまり、体心立方では、
$生身のゴリラ1人 + \frac{1}{8}メカゴリラ × 8$
で、けっきょく2人のゴリラがいることになるウホ!というわけで、体心立方ゴリライトのなかにはゴリラが2人分いることになるウホ。
…
おなじように、ゴリライトBとして面心立方ゴリライトについても考えるウホ。面心立方ゴリライトの図はさっき上にも書いた通りウホ。
おなじようにかんがえると、面心立方ゴリライトには、8カドに$\frac{1}{8}$ゴリラ、6つの面には$\frac{1}{2}$ゴリラがいるウホ。ということは、全部メカゴリラだとかんがえて、ばらばらにしてからもとにもどすとすると、
$(\frac{1}{2}メカゴリラ × 6) + (\frac{1}{8}メカゴリラ × 8)$
で、けっきょく4人のゴリラがいることになるウホ!
こたえ:ゴリライトAは2ゴリラ分、ゴリライトBは4ゴリラ分がふくまれる
ちなみに、面心立方格子は金(Au)、体心立方格子はナトリウム(Na)とかが当てはまるウホ。
ゴリライト💎としてそれぞれの格子構造🎲をかんがえてみたけど、じっさいにゴリライトがどのようなせいしつをもっているとよさそうなのか、じっくり考えていきたいウホ。