ゴリラと学ぶ「円順列」
ゴリがジャングルをさんぽ👣していると、5人のゴリラがなにやら集まっていたウホ。
なにをしているのかきいてみると、5人のゴリラたちは召喚、つまり外の世界からなにかをよびだそうとしているみたいだウホ。
ほんとにそんなことができたら、すごいことだウホ。ゴリもさっそく召喚するようすをみてみたいとおもったウホ。
そのまえに、ゴリ的には、この5人のゴリラの組み合わせで、どれくらいの召喚のパターンがあるか気になったウホ。
さっそく、どれくらいのパターンがあるか、計算してみることにしたウホ。
もんだい
5人のゴリラサモナー🦍が、ひとつの輪🍩になってなにかを召喚しようとするばあいを考えるウホ。
このゴリラサモナーは、5人のならべかたによって、召喚できるやつがちがうウホ。
すると、5人がわっかになるとき、そのならべかたは何通りあるウホ？
ただし、ゴリラはすべて、ゴリラA、ゴリラBみたいに、個体を区別できるものとするウホ。
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
なにをしょうかんするのかわからないけど、とりあえずけいさんするウホ！
ニンゲンが高校数学でならう、順列にかんするちしきをかつようするウホ。
まず、5人のゴリラがわっかにならぶ場合の数は、通りあるウホ。
いいかえる、というかべつの書き方をすると、順列のかきかただと（5人のゴリラから5人をえらぶ）、階乗のかきかたでかくと、通りあることになるウホ。階乗とは、その数（自然数）から1ずつへった数をかけていくほうほうだったウホ。
で、120とおりでゴリたちがわっかになると考えるけど、ちょっとまつウホ。
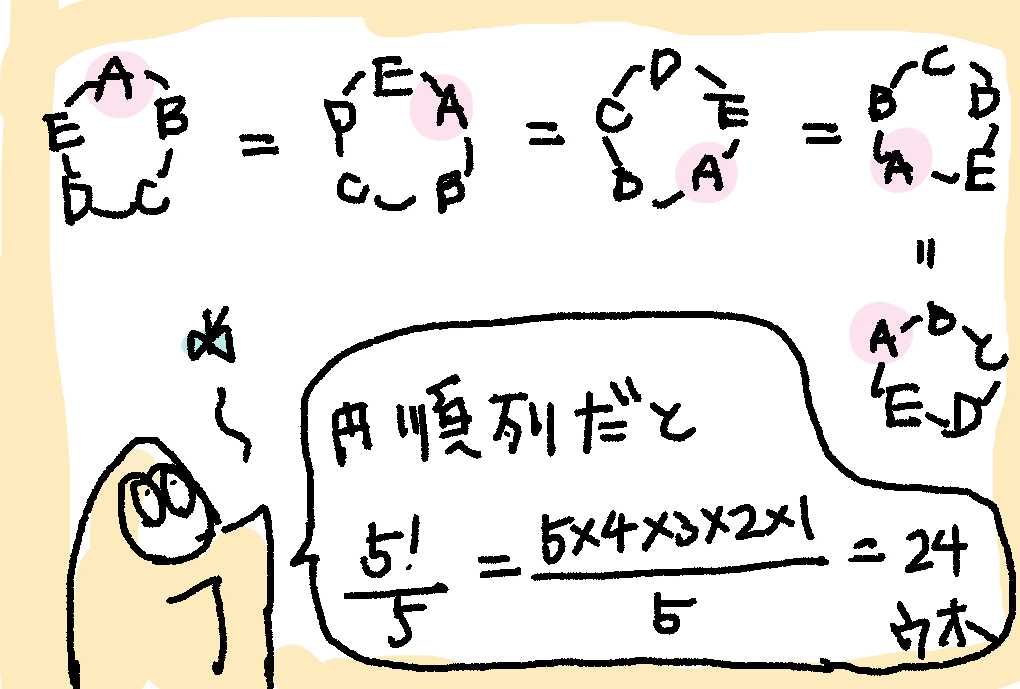
5人のゴリラたち（A, B, C, D, E）がわっかになって、くるくるとかいてんするとかんがえるウホ。
もとのAがいた位置にBが、Bがいた位置にCが・・・というかんじで、場所をかえたとするウホ。
ぱっと見ではいちがかわって、ちがうわっか🍩にそうだけど、じっさいにはゴリラたちのじゅんばんはかわってないウホ！
そうすると、5人のゴリラたちは五ずつずれてもおなじ順番だから、
ひとつのならびかたにつき5個ぶん重複していることになるウホ。つまり、おなじものなのにちがうものとして数えちゃっていたウホ。
だから、1つのわっかにつき5通りぶん重複していたから、これを割り算するウホ。
ぜんぶで24通りになったウホ！
こたえ： 24通り
このゴリラたちは、24通りもの召喚パターンがあることになるウホ！
さっそく、どんなやつが召喚されるのか、見させてもらうウホ。
✨🦍🦍🦍🦍🦍✨
✨✨
✨
・・・
✨ 🦍🐎 ✨
なんと！ゴリケンタウロス🦍🐎がしょうかんされたウホ！すごいことだウホ！
あれ？でもこのゴリケンタウロスは、まえにゴリゴリ算のときも触れたように、２人のゴリラ🦍🦍が合体しただけのすがただったウホ。
どうやら、こんかいはしっぱいしちゃったみたいだウホ。つぎの召喚にきたいしたいウホ。