ゴリラと学ぶ「作図」垂直二等分線編

ゴリたちゴリラ🦍は、木🌲を自分のものとすることがおおいウホ(「三角比で木の上からゴリラのきょりをはかるウホ」とか)。じっさいのゴリラ(?)はそうかはしらないけど、とりあえずゴリたちはそうしているウホ。
だから、木と木の間は、けっこうナワバリあらそいのタネ🌱になるウホ。この領域を、しろくろ🐼はっきりさせたいウホ。
こんかいは、ゴリラのナワバリについて、木からの距離ををちゅうしんとしてかんがえてみるウホ。
もんだい
あるゴリラ🦍たちが、じぶんたちのナワバリについてそうだんしていたウホ。
いままではなんとなくきめてきていたけど、もうちょっとおつむ🧠をつかってかんがえてみたいウホ。
それぞれのゴリラは、自分たちの木をもっているとするウホ。木は、ゴリラにつき1本あるとするウホ。
木と木の間の距離は、そこそこはなれていて、そのあいだにはとくにじゃまなものはなく、平らな土地だとするウホ。
ぐたいてきにはしたみたいなかんじウホ。ゴリラの木○と、ゴリラの木じゃないの●もまざっているウホ。
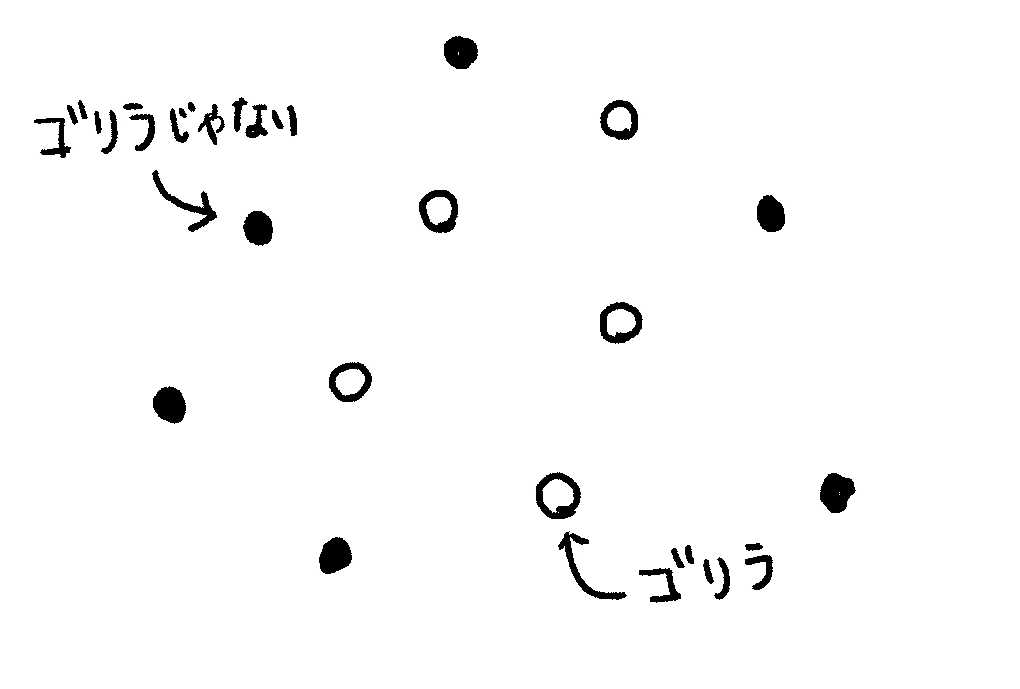
このゴリラたちの、木のナワバリを決めるには、どうすればいいウホ?
🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲
かいとうあん
いろいろこたえはあるとおもうけど、いちばんシンプルなほうほうでかんがえるウホ。
ニンゲンはちゅうがっこうで、垂直二等分線について、コンパスで作図するやつをべんきょうしたとおもうウホ。
ラグビーボール🏉みたいたかたちの線を、2点をむすんだ直線に垂直にひいて、そこへ縦にちょくせんをひくことで作図していたウホ。
で、この垂直二等分線は、そのなのとおり、辺を二等分する直線だったウホ。
いいかえると、垂直な線から2点の距離はひとしかったウホ。
これをつかうことで、二つのナワバリの木から等しい距離にある直線がひけて、その交点は、これもナワバリの木からの距離が等しいウホ。
こんなかんじに、ある三角形のかくへんの垂直二等分線をひくと、その垂直二等分線どうしの交点は、どれも三角形のどの角からもひとしい距離にあることになるウホ。
ちなみにこの点は、その三角形に外接する(三角形の外側でせっする)円の中心(=外心)になるウホ。
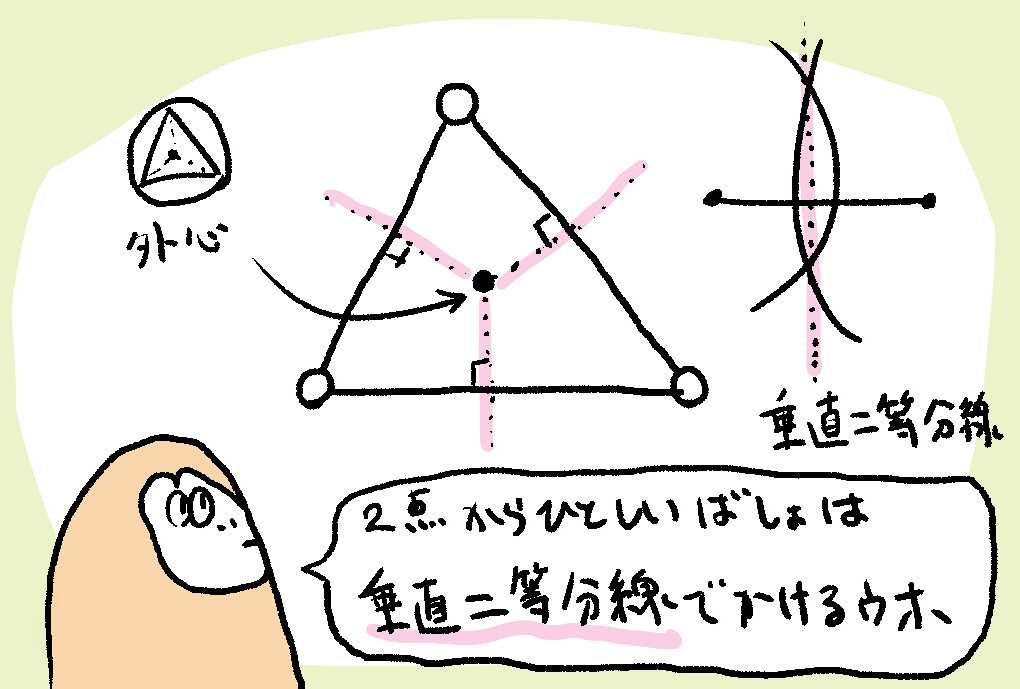
さておき、三角形の各点からひとしいきょりにある線がかけるようになったウホ。
これを、ほかのすべての三角形にもつかっていくウホ。
ほんで、べつの三角形の垂直二等分線とも合体させたり、いちど交点ができたらその先はのばさないようにしたり、とにかくいろいろやるウホ。
こうすることで、ゴリラのナワバリについて、それぞれの木から等しい距離にある線をひくことができたウホ!
下の図はちょっとてきとうにかいたところもあるからさんこうていどにするウホ。
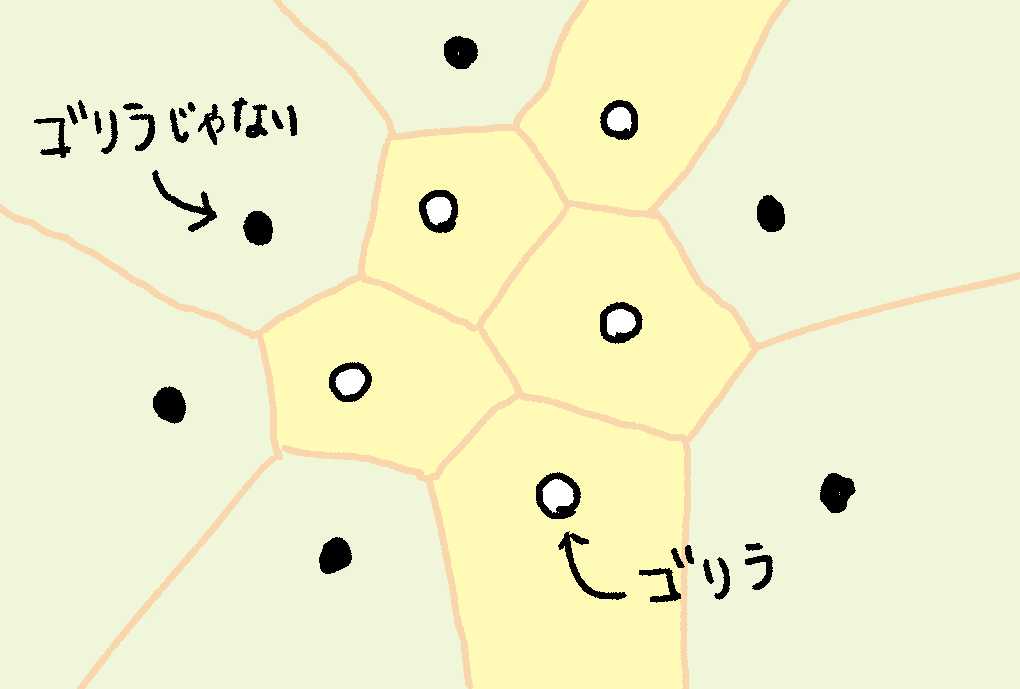
これは、ニンゲンのせかいではボロノイ図とよばれる図形だそうだウホ。Wikipediaによると学校の校区を決めたり、無線通信の基地局のばしょをきめたり、なんかいろいろつかわれているらしいウホ。
これで、ひとまずゴリラのナワバリについて決めることができたウホ!
こたえ:上の図のとおり
このボロノイ図📐で、ゴリラ🦍たちのナワバリについて考えることができたウホ。
でも、はしっこのゴリラは、けっこういいナワバリをもっているウホ。
こういうゴリラたちにも平等にナワバリを決めることができるほうほうもかんがえていきたいウホ。