ゴリラと学ぶ「球の体積」半球編

ジャングル🌲を歩いていると、のどがからから🌞になることがあるウホ。
さばく🏜じゃないにせよ、ゴリはいきているうちにい水💧をどんどんつかうから、のどもどんどんかわいていく🌞ウホ。
そんなときに、滝💧をみつけたウホ!せっかくだから、ゴリは手にもっているおおきなおけ🥣に水💧をとることにしたウホ。
滝といいつつも、けっこういきおいがあって大きい滝だから、ゴリはたきのわきにあるちいさな滝から水をとることにしたウホ。
こんかいは、この滝💧から水をとるじかん🕓をけいさんするウホ。
もんだい
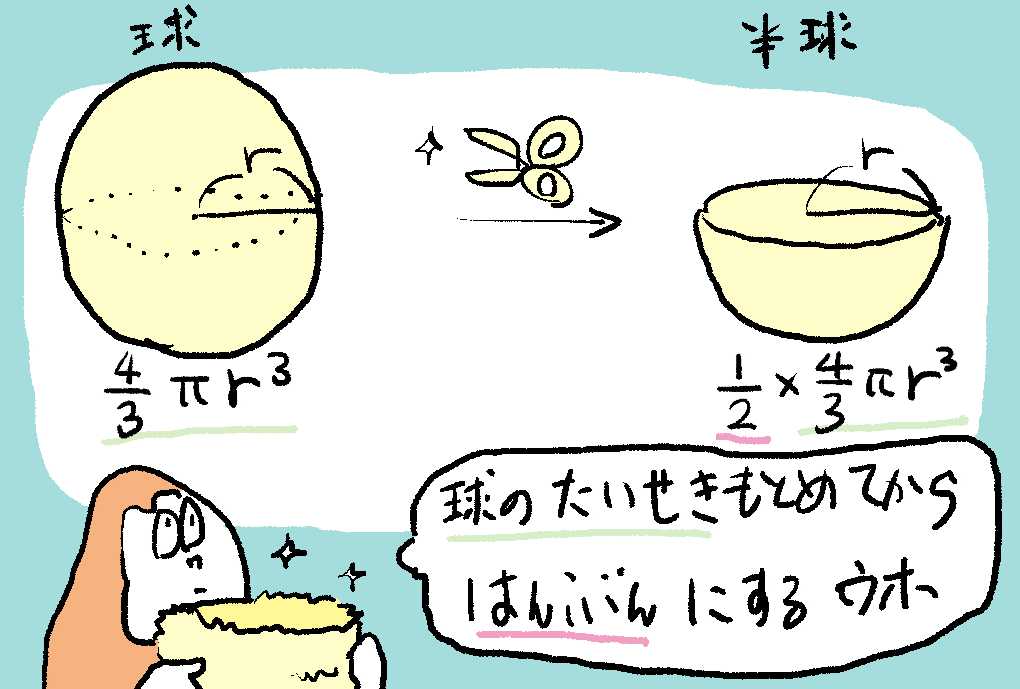
ゴリは半球のおけをもっているウホ。半球とは、たま🥎をはんぶんにしたかたちウホ。
このおけは、半径が20 cmウホ。
また、小さな滝からは、毎秒1Lの水がでているとするウホ。
ところが、たいへんウホ!ゴリはもよおしちゃって、おしっこをしたくなっちゃったウホ!
いそげば15秒でできるから、せっかくだし、おけに水を入れ始めてからおしっこしたいウホ。
おけは、ふわふわの羽毛🐦でデコレーション✨しているから、できればぬらしたくないウホ。
水におけがいっぱいになった、ちょうどそのときに回収したいウホ。
このとき、おけが水でいっぱいになるには、何秒かかるウホ?
また、ゴリはおしっこがおわるまでにおけに水を入れ終わるウホ?
ただし、ざっと暗算しやすいように、円周率π = 3とするウホ。
また、$1 cm^3 = 1 mL$とするウホ。
💧💧💧💧💧💧💧💧💧💧💧💧💧
こたえ
まずはおけ(半球)にはいる水の体積をしらべるウホ。
球の体積の公式をつかうウホ!球の体積のこうしきは次の通りだったウホ。
$球の体積 = \frac{4}{3} πr^3$
ここで、$r = 球の半径$とするウホ。
けいさんをかんたんにするために、π = 3としていたウホ。そして、球の半径は20 cmだったウホ。
このことから、おけのたいせきは、まず球のばあいは次のとおりになるウホ。
$おけの体積(球のばあい) = \frac{4}{3} × 3 × 20^3 = 4 × 20^3 = 32000 cm^3$
そして、じっさいには半球だから、それを2分の1とするウホ。
$おけの体積(半球) = おけの体積(球のばあい)/ 2 = 16000 cm^3$
そして、$cm^3$とL(リットル)をへんかんするウホ!
$1 cm^3 = 1 mL = \frac{1}{1000} L$
だから、$16000 cm^3 = 16 L$になるウホ。
つぎに、どれくらいのじかんでいっぱいになるか考えるウホ。
これは、たんじゅんに、小さな滝からは1秒間に1Lでてくるから、
$16 L ÷ \frac{1 L}{1秒} = 16秒$
こたえは16秒になったウホ!つまり、ゴリがおしっこしてからもどってくる15秒でぎりぎりまにあうウホ。
こたえ: 16秒、ゴリがおしっこしてからもどってきてもまにあう
こんなことしなくても、さきにおしっこしてからゆっくりお水💧をとればいいウホ。
でも、ゴリのぼうこうはひめい😱をあげていたウホ。そして、ピンチの時は、だれしもれいせいな判断ができなくなるウホ。
ゴリは、いそいでもどってきて、おけ🥣に水💧がちょうどはいったことをかくにんしたウホ。
ほっとひとあんしんして、て👐をあらうのをわすれて、そのまま水を手に取ってのどのかわき🌞をうるおしたウホ。