ゴリラと学ぶ「標本調査」ゴリラの数編

ゴリラ🦍たちのいるジャングル🌲は、とても広大だウホ。このジャングルの中にはたくさんゴリラがいるらしいけれど、ちゃんとはかったことはないウホ。一人ひとりの数を数えていくのも、とても大変だウホ。
まったくかんぺきに知らなくてもいいけど、だいたいのゴリラ🦍の数を知りたいとするウホ。そこで、ゴリはつぎのようなほうほうをやってみたウホ。
もんだい
あるジャングルの一区画に、ゴリラがたくさんいる🦍🦍🦍🦍🦍ウホ。 ぜんぶの人たちをたずねあるくのは、すこしめんどうだウホ。
そこでゴリは、まずはがんばって、500人のゴリラ🦍を呼びあつめたウホ。そして、みんなに赤いリストバンド🍎をつけてもらったウホ。
そのあと、このゴリラたちをジャングルに返してから、もういちどゴリラたちを呼び集めたウホ。
すると、リストバンドをしたゴリラ🍎が25人、リストバンドをしていないゴリラ🍐が55人の、あわせて80人があつまったウホ。
このとき、このジャングルの一区画にいるゴリラは、だいたいどれくらいウホ?
ただし、ジャングルのなかには、ゴリラはきんとうにばらけていると仮定するウホ。
そして、呼んであつまってくるゴリラはランダムだと仮定するウホ。
🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍🌲🦍
こたえ
中学数学の、標本調査👬のかんがえかたをつかうウホ。標本調査では、あるしゅうだんの一部👬をしらべることで、集団全体(母集団)👬👬👬👬がどうなっているのか調べるほうほうだったウホ。
ぜんぶのゴリラを一人ずつかぞえていくのは、全数調査というほうほうだけれど、こんかいは標本調査をやるウホ。
標本調査では、しゅうだんぜんたいの数を$x$とおくウホ。このとき、つぎのような関係があるウホ。
$\frac{最初にとってきて印つけた数}{母集団の数(x)} = \frac{2かいめの印ついてた数}{2かいめの全部の数}$
今回のばあいは、
$\frac{最初に赤🍎つけたゴリラ}{全ゴリラ} = \frac{2かいめの赤つけたゴリラ}{2かいめの全部のゴリラ}$
になるウホ。
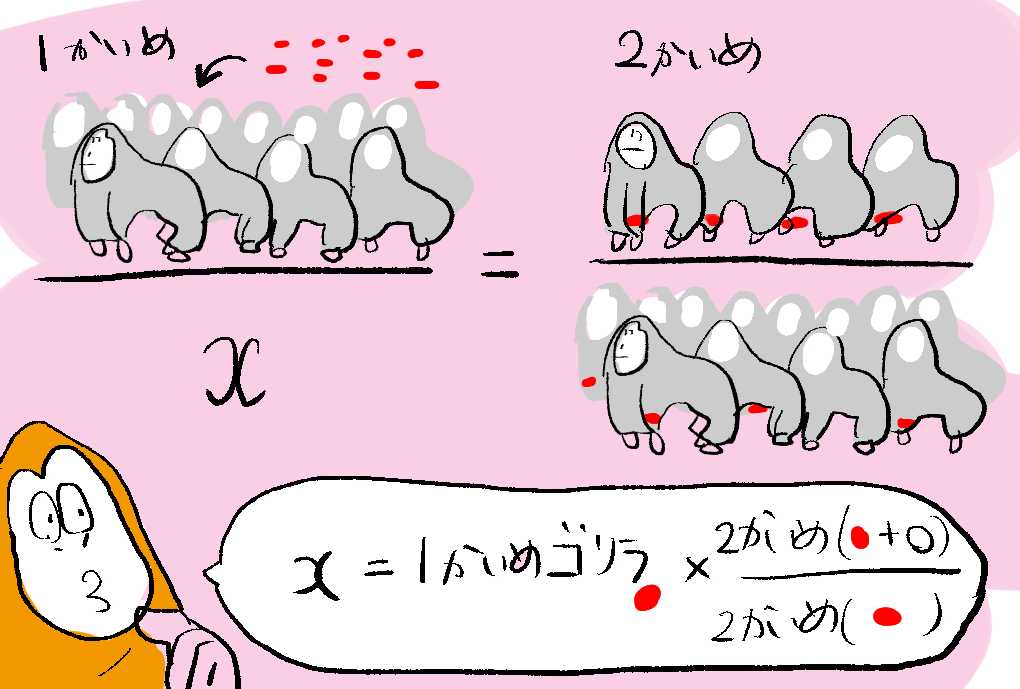
ぐたいてきに数をいれていくウホ。
$\frac{500}{x} = \frac{25}{80}$
そうすると、$x$ = 1600となったウホ。
このジャングルの中には、すごくざっくりとだけど、だいたい1600人のゴリラ🦍がいることがわかったウホ!
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ: だいたい1600人いる
ニンゲンのしゃかいだと、世論調査📚なんかにもつかわれている✏ほうほうウホ。
今回のような、いっかいのちょうさだと、たまたま1600人になったかのうせいもあるウホ。そのあたりを工夫して、もっとたしからしいゴリラ🦍の数がわかるようなほうほうを調べていきたい👊🦍👊ウホ。
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍